

So stay tuned, I will be posting some new Logo programs after I refined some language issues. And in fact, I have identified a few bugs and new ideas that I need to implement in VRMath2 Editor. My purpose of doing this hypercube is to test the CoordinateInterpolator for animation. I have not yet to write teaching and learning ideas for this, but I think students will be interested in creating and programming, and at the same time learnt about 3D coordinate system and structure of cubes.
#Rotating hypercube movie#
Only if you are interested, you can download and try the Logo program here: hypercube.logo.įrom doing this, the mathematical concepts about zero to n-dimension space can be explored. The movie depicts a rotating spacetime hypercube, projected from 4 dimensions on to the 2 dimensions of the screen in the same way as the rotating 4D hypercube.The prototypical example of a hypercube is the 4-dimensional geometrical object with corners at (t, x, y, z) (☑, ☑, ☑, ☑). You can click on it to toggle the spin effect on and off. I have also added a small sphere at the center of the hypercube. You can see below how the 4D cube was created from 0-D point to 1-D line, to 2-D square, to 3-D cube, then to 4-D Tesseract. I tried in VRMath2 Editor to create a 4D cube. You may also study in more depth on Wikipedia, where you can find the mathematical n-dimensional hypercubes. One of the most famous 4D cubes is perhaps the 4D Cube building in Paris. The 4th dimension here is not about time, but the beauty of the abstract geometrical dimensions that exist in the mathematical world. The Hypercube: Projections and Slicing was awarded the Prix de la Recherche Fondamentale at the 1978 International Congress of Scientific Films.I am always fascinated by the visualisation of 4th dimension or even n-th dimension in our 3D space. That w-axis (in blue) is representative of a direction that’s perpendicular to height, length, and width, and can be best understood in the motion of the film. It can now move in three directions: left and right (x-direction), up and down (y-direction) and back and forth (z-direction).”Īllowing the point more freedom, beyond our 3D world, moves it in four directions: left and right (x-direction), up and down (y-direction), back and forth (z-direction), ana and kata (w-direction). The point is happy because it can travel even more. Moving the square perpendicular to itself results in a cube. The point can now travel left and right as well as up and down.
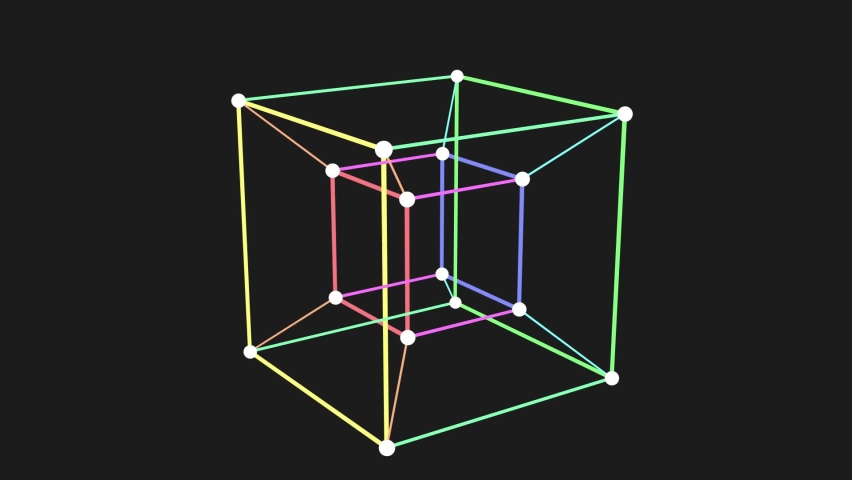
“Now we move the line perpendicular to itself in a plane and we get a square. It is now possible for the zero-dimensional point to travel within the line in a left and right manner. If we put another point at the right side beside the first one and connect them we get a line. It only exists in itself and has no possibilities to move anywhere. “To get an idea of the fourth dimension maybe it would be a good start to begin with a point. The extra dimension is added due to the geometrical laws found in the first three…” It is constructed with mathematical means by analyzing three-dimensional space and how the three dimensions relate to each other. Try to think of it as geometrical extravaganza. Download this stock image: 4 Dimensional Hypercube Tesseract Rotating in Outer Space and Stars - Abstract Background Texture - 2C3XJ1H from Alamys library. It’s a concept of an artificial space that bears no direct similarity to real space. “There is no fourth dimension in reality.
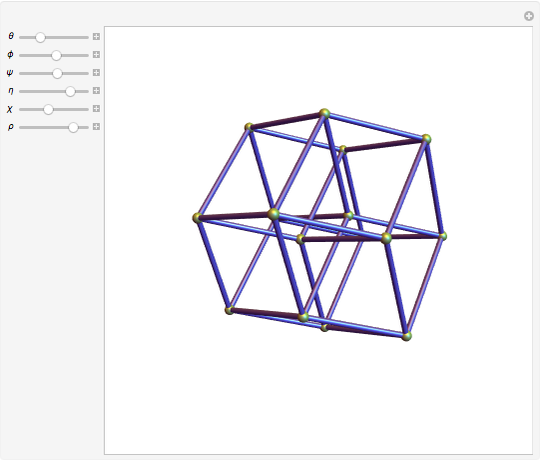
The resulting film, titled The Hypercube: Projections and Slicing, was constructed with the real-time interactive computer graphics of the era, a technological milestone for 4-dimensional geometry.īeginning at the 1-minute mark, the film observes and annotates a rotating cube in three ways: orthogonal or straight projection, central or perspective projection, and finally with hyperplane slices coming from four different directions.

“The tesseract can be unfolded into eight cubes into 3D space, just as the cube can be unfolded into six squares into 2D space.” In 1978, mathematics professor Thomas Banchoff and computer scientist Charles Strauss teamed up to create an animated visualization of a 3-dimensional cube rotating in four-dimensional space, also known as a hypercube or tesseract.


 0 kommentar(er)
0 kommentar(er)
